Note
Click here to download the full example code
Reproducing the simulations from Foygel-Barber et al. (2020)¶
MapieRegressor is used to investigate
the coverage level and the prediction interval width as a function
of the dimension using simulated data points as introduced in
Foygel-Barber et al. (2021) [1].
This simulation generates several times linear data with random noise whose signal-to-noise is equal to 10 and for several given dimensions.
Here we use MAPIE, with a LinearRegression base model, to estimate the width means and the coverage levels of the prediction intervals estimated by all the available strategies as function of the dataset dimension.
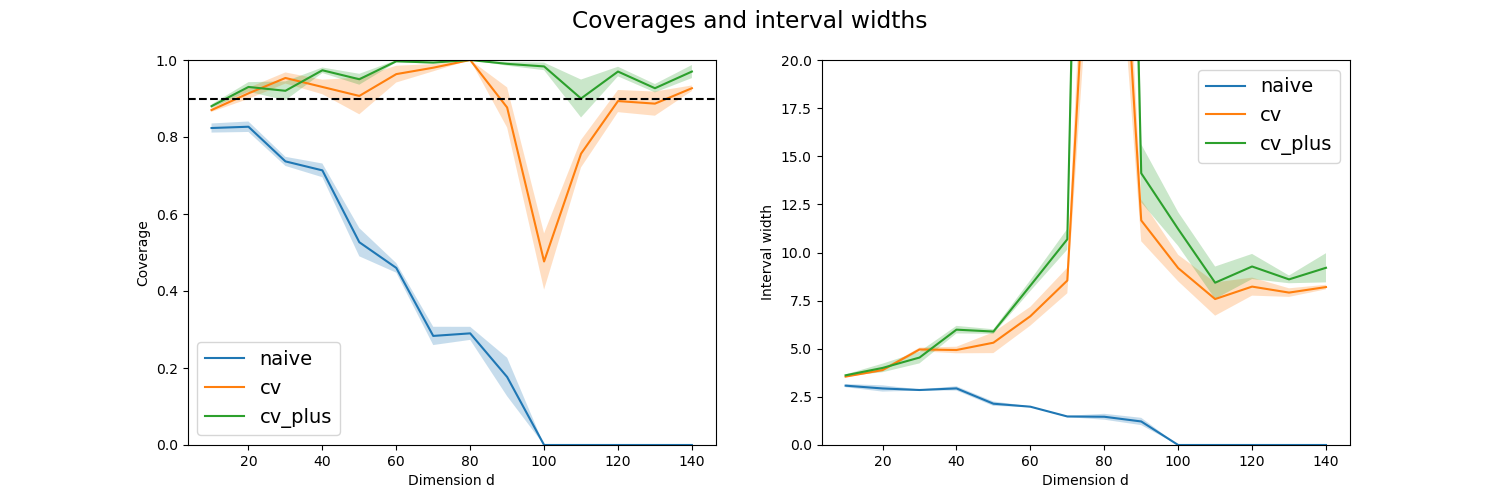
We then show the prediction interval coverages and widths as a function of the dimension values for selected strategies with standard error given by the different trials.
This simulation is carried out to emphasize the instability of the prediction intervals estimated by the jackknife strategy when the dataset dimension is equal to the number of training samples (here 100).
[1] Rina Foygel Barber, Emmanuel J. Candès, Aaditya Ramdas, and Ryan J. Tibshirani. “Predictive inference with the jackknife+.” Ann. Statist., 49(1):486–507, February 2021.
from typing import Any, Dict
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from mapie._typing import NDArray
from mapie.metrics import (regression_coverage_score,
regression_mean_width_score)
from mapie.regression import MapieRegressor
def PIs_vs_dimensions(
strategies: Dict[str, Any],
alpha: float,
n_trial: int,
dimensions: NDArray,
) -> Dict[str, Dict[int, Dict[str, NDArray]]]:
"""
Compute the prediction intervals for a linear regression problem.
Function adapted from Foygel-Barber et al. (2020).
It generates several times linear data with random noise whose
signal-to-noise is equal to 10 and for several given dimensions,
given by the dimensions list.
Here we use MAPIE, with a LinearRegression base model, to estimate
the width means and the coverage levels of the prediction intervals
estimated by all the available strategies as a function of
the dataset dimension.
This simulation is carried out to emphasize the instability
of the prediction intervals estimated by the Jackknife strategy
when the dataset dimension is equal to the number
of training samples (here 100).
Parameters
----------
strategies : Dict[str, Dict[str, Any]]
List of strategies for estimating prediction intervals,
with corresponding parameters.
alpha : float
1 - (target coverage level).
n_trial : int
Number of trials for each dimension for estimating
prediction intervals.
For each trial, a new random noise is generated.
dimensions : List[int]
List of dimension values of input data.
Returns
-------
Dict[str, Dict[int, Dict[str, NDArray]]]
Prediction interval widths and coverages for each strategy, trial,
and dimension value.
"""
n_train = 100
n_test = 100
SNR = 10
results: Dict[str, Dict[int, Dict[str, NDArray]]] = {
strategy: {
dimension: {
"coverage": np.empty(n_trial),
"width_mean": np.empty(n_trial),
}
for dimension in dimensions
}
for strategy in strategies
}
for dimension in dimensions:
for trial in range(n_trial):
beta = np.random.normal(size=dimension)
beta_norm = np.sqrt(np.square(beta).sum())
beta = beta / beta_norm * np.sqrt(SNR)
X_train = np.random.normal(size=(n_train, dimension))
noise_train = np.random.normal(size=n_train)
noise_test = np.random.normal(size=n_test)
y_train = X_train.dot(beta) + noise_train
X_test = np.random.normal(size=(n_test, dimension))
y_test = X_test.dot(beta) + noise_test
for strategy, params in strategies.items():
mapie = MapieRegressor(
LinearRegression(),
agg_function="median",
n_jobs=-1,
**params
)
mapie.fit(X_train, y_train)
_, y_pis = mapie.predict(X_test, alpha=alpha)
coverage = regression_coverage_score(
y_test, y_pis[:, 0, 0], y_pis[:, 1, 0]
)
results[strategy][dimension]["coverage"][trial] = coverage
width_mean = regression_mean_width_score(
y_pis[:, 0, 0], y_pis[:, 1, 0]
)
results[strategy][dimension]["width_mean"][trial] = width_mean
return results
def plot_simulation_results(
results: Dict[str, Dict[int, Dict[str, NDArray]]], title: str
) -> None:
"""
Show the prediction interval coverages and widths as a function
of dimension values for selected strategies with standard error
given by different trials.
Parameters
----------
results : Dict[str, Dict[int, Dict[str, NDArray]]]
Prediction interval widths and coverages for each strategy, trial,
and dimension value.
title : str
Title of the plot.
"""
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
plt.rcParams.update({"font.size": 14})
plt.suptitle(title)
for strategy in results:
dimensions = list(results[strategy].keys())
n_dim = len(dimensions)
coverage_mean = np.zeros(n_dim)
coverage_SE = np.zeros(n_dim)
width_mean = np.zeros(n_dim)
width_SE = np.zeros(n_dim)
for idim, dim in enumerate(dimensions):
coverage = results[strategy][dim]["coverage"]
coverage_mean[idim] = coverage.mean()
coverage_SE[idim] = coverage.std() / np.sqrt(ntrial)
width = results[strategy][dim]["width_mean"]
width_mean[idim] = width.mean()
width_SE[idim] = width.std() / np.sqrt(ntrial)
ax1.plot(dimensions, coverage_mean, label=strategy)
ax1.fill_between(
dimensions,
coverage_mean - coverage_SE,
coverage_mean + coverage_SE,
alpha=0.25,
)
ax2.plot(dimensions, width_mean, label=strategy)
ax2.fill_between(
dimensions,
width_mean - width_SE,
width_mean + width_SE,
alpha=0.25,
)
ax1.axhline(1 - alpha, linestyle="dashed", c="k")
ax1.set_ylim(0.0, 1.0)
ax1.set_xlabel("Dimension d")
ax1.set_ylabel("Coverage")
ax1.legend()
ax2.set_ylim(0, 20)
ax2.set_xlabel("Dimension d")
ax2.set_ylabel("Interval width")
ax2.legend()
STRATEGIES = {
"naive": dict(method="naive"),
"cv": dict(method="base", cv=5),
"cv_plus": dict(method="plus", cv=5),
}
alpha = 0.1
ntrial = 3
dimensions = np.arange(10, 150, 10)
results = PIs_vs_dimensions(STRATEGIES, alpha, ntrial, dimensions)
plot_simulation_results(results, title="Coverages and interval widths")
plt.show()
Total running time of the script: ( 0 minutes 10.284 seconds)