Theoretical Description for Conformity Scores¶
The mapie.conformity_scores.ConformityScore class implements various
methods to compute conformity scores for regression.
We give here a brief theoretical description of the scores included in the module.
Note that it is possible for the user to create any conformal scores that are not
already included in MAPIE by inheriting this class.
Before describing the methods, let’s briefly present the mathematical setting.
With conformal predictions, we want to transform a heuristic notion of uncertainty
from a model into a rigorous one, and the first step to do it is to choose a conformal score.
The only requirement for the score function 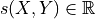 is
that larger scores should encode worse agreement between
is
that larger scores should encode worse agreement between 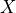 and
and 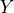 . [1]
. [1]
There are two types of scores : the symmetric and asymmetric ones. The symmetric property defines the way of computing the quantile of the conformity scores when calculating the interval’s bounds. If a score is symmetrical two quantiles will be computed : one on the right side of the distribution and the other on the left side.
1. The absolute residual score¶
The absolute residual score (mapie.conformity_scores.AbsoluteConformityScore)
is the simplest and most commonly used conformal score, it translates the error
of the model : in regression, it is called the residual.
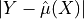
The intervals of prediction’s bounds are then computed from the following formula :
![[\hat{\mu}(X) - q(s), \hat{\mu}(X) + q(s)]](_images/math/a7365e86ddd51c4e8e810fd453e226e36b817790.png)
Where 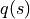 is the
is the 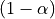 quantile of the conformity scores.
(see Theoretical Description for more details).
quantile of the conformity scores.
(see Theoretical Description for more details).
With this score, the intervals of predictions will be constant over the whole dataset. This score is by default symmetric (see above for definition).
2. The gamma score¶
The gamma score [2] (mapie.conformity_scores.GammaConformityScore) adds a
notion of adaptivity with the normalization of the residuals by the predictions.
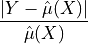
It computes adaptive intervals : intervals of different size on each example, with the following formula :
![[\hat{\mu}(X) * (1 - q(s)), \hat{\mu}(X) * (1 + q(s))]](_images/math/34ea26287318258d1caf28365fdb302c9f5b37b3.png)
Where 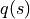 is the
is the 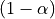 quantile of the conformity scores.
(see Theoretical Description for more details).
quantile of the conformity scores.
(see Theoretical Description for more details).
This score is by default asymmetric (see definition above).
Compared to the absolute residual score, it allows us to see regions with smaller intervals than others which are interpreted as regions with more certainty than others. It is important to note that, this conformity score is inversely proportional to the order of magnitude of the predictions. Therefore, the uncertainty is proportional to the order of magnitude of the predictions, implying that this score should be used in use cases where we want greater uncertainty when the prediction is high.
3. The residual normalized score¶
The residual normalized score [1] (mapie.conformity_scores.ResidualNormalisedScore)
is slightly more complex than the previous scores.
The normalization of the residual is now done by the predictions of an additional model
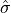 which learns to predict the base model residuals from
which learns to predict the base model residuals from 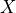 .
.
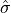 is trained on
is trained on 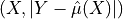 and the formula of the score is:
and the formula of the score is:
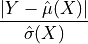
This score provides adaptive intervals : intervals of different sizes in each point with the following formula :
![[\hat{\mu}(X) - q(s) * \hat{\sigma}(X), \hat{\mu}(X) + q(s) * \hat{\sigma}(X)]](_images/math/1d81f1fba41634eaeebd7ec2611f8f73765b9241.png)
Where 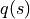 is the
is the 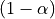 quantile of the conformity scores.
(see Theoretical Description for more details).
quantile of the conformity scores.
(see Theoretical Description for more details).
This score is by default symmetric (see definition above). Unlike the scores above, and due to the additional model required this score can only be used with split methods.
Normalization by the learned residuals from 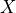 adds to the score a knowledge of
adds to the score a knowledge of
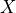 and its similarity to the other examples in the dataset.
Compared to the gamma score, the other adaptive score implemented in MAPIE,
it is not proportional to the uncertainty.
and its similarity to the other examples in the dataset.
Compared to the gamma score, the other adaptive score implemented in MAPIE,
it is not proportional to the uncertainty.
Key takeaways¶
The absolute residual score is the basic conformity score and gives constant intervals. It is the one used by default by
mapie.regression.MapieRegressor.The gamma conformity score adds a notion of adaptivity by giving intervals of different sizes and is proportional to the uncertainty.
The residual normalized score is a conformity score that requires an additional model to learn the residuals of the model from
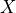 . It gives very adaptive intervals
without specific assumptions on the data.
. It gives very adaptive intervals
without specific assumptions on the data.
References¶
[1] Lei, J., G’Sell, M., Rinaldo, A., Tibshirani, R. J., & Wasserman, L. (2018). Distribution-Free Predictive Inference for Regression. Journal of the American Statistical Association, 113(523), 1094–1111. Available from https://doi.org/10.1080/01621459.2017.1307116
[2] Cordier, T., Blot, V., Lacombe, L., Morzadec, T., Capitaine, A. & Brunel, N.. (2023). Flexible and Systematic Uncertainty Estimation with Conformal Prediction via the MAPIE library. Available from https://proceedings.mlr.press/v204/cordier23a.html.